200以上 分数の解き方 582607-分数の解き方
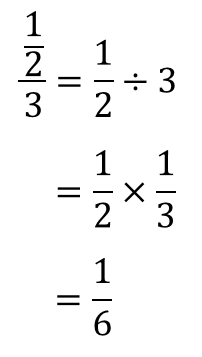
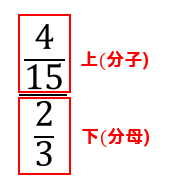
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
フランスの数学者、 アンリ・ポアンカレ は「分数とは横線によって画された2つの整数の集合であって、この記号によって施すことができる演算を規約によって定義する」と説明している 5 。② 分数×分数の計算のしかた ③ 逆数の意味と逆数の求め方 ④ 分数倍の意味と分数倍を使った割合の考え方、分数の積の大きさ 教え方1 はじめに小数×整数(4年)のおさらいをさせましょう。 問題①4
分数の解き方
分数の解き方-分数は(分子)÷(分母)で表せる。 分数の基本的な考え方を思い出して欲しいのですが 割り算はこのように分数の形で表すことができましたよね。 これを逆に考えれば 分数も当然、割り算の形で 分数の割り算はひっくり返す! 分数の割り算は、たった一つの動作で掛け算に変身します。 割る数の分子と分母を逆にする これだけです! そうすれば、÷を×に変えることができます
分数の 28n 3が自然数になるような最も小さい自然数nの値を求める問 Yahoo 知恵袋
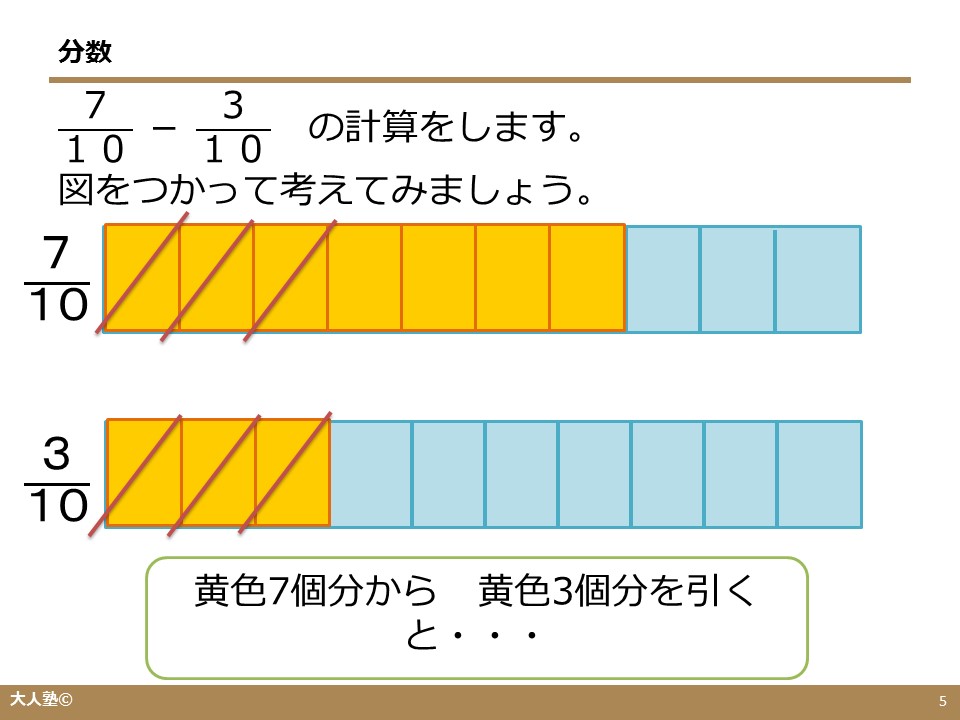
特に「逆数」の理解が不十分な場合は、↓でおさらいしましょう。 6年「逆数」の教え方 ①分数÷整数の計算の意味と計算方法 ②分数÷分数の計算の意味と計算方法 ③分数倍を使った割合の考え方 次のような分数の場合は 答えはどのようになるのでしょうか? 頑張って チャレンジしてみて下さい。 どうだったでしょうか? それでは 解き方を見ていきます。 考え方は 今までと同整数の部分と分数の部分を分けて、分数の部分は分子÷分母を計算します。 よって答えは 225 まとめ 分数は「何個に切ったうちの何個分」と考えて、だいたいの大きさをイメージするようにする。
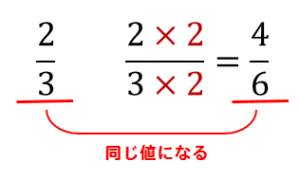
難易度の低いものは、分数の定義から出発すればできますが、難易度の高いものは工夫が必要です。 以下の順に分けて説明していきます。 分母が等しい場合 分子が等しい場合 応用分数には 「分母・分子に同じ数をかけても分数の値は変わらない」 という性質があるのでこれを利用するのです。 具体的には、分母の公倍数を見つけて、その数字に分母を揃えるようにそれぞれの 2 分数の微分のやり方 結論から言うと、分数の微分はどちらも公式を使って求めることができます。それぞれ見ていきましょう。 分数の微分公式 まず、分母が関数である場合の微分は
分数の解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | ||
 |  | |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 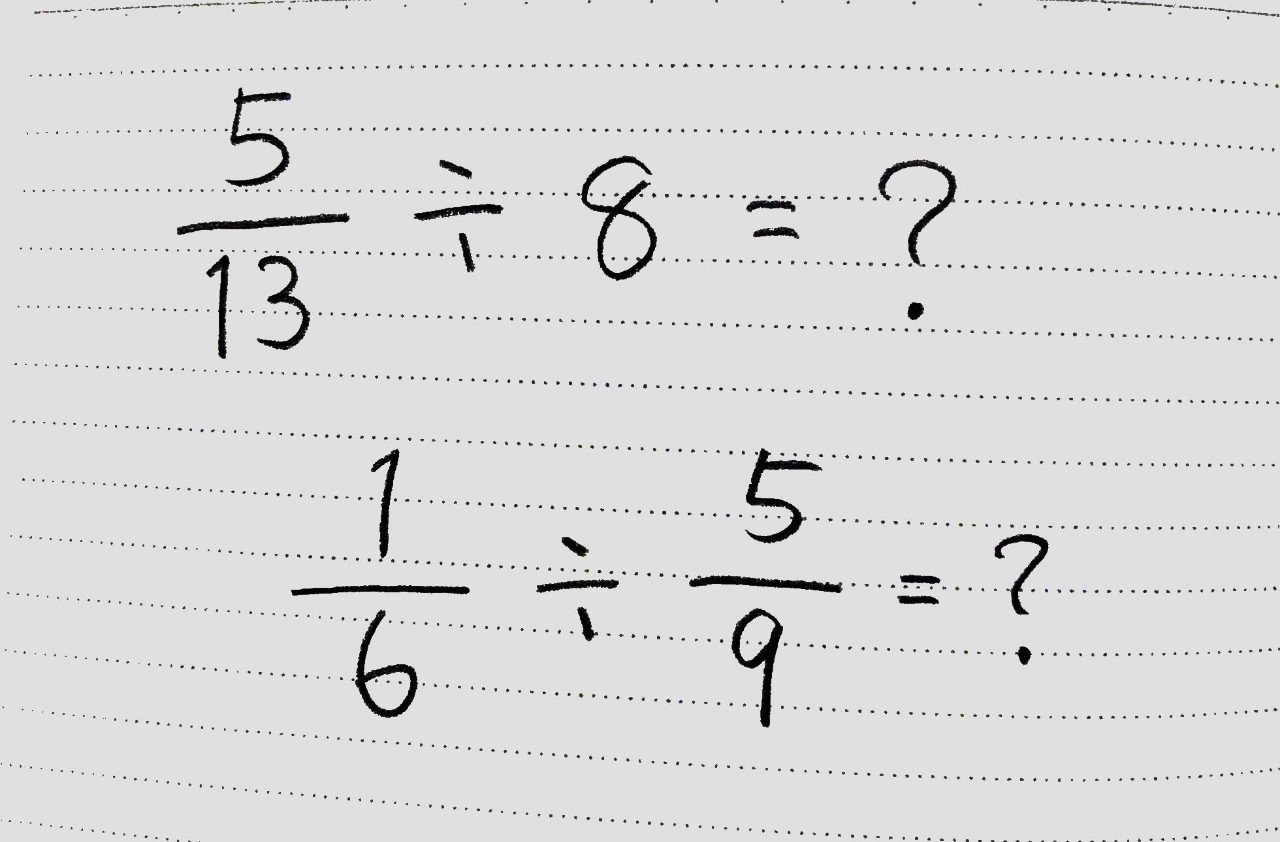 | |
 |  | |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
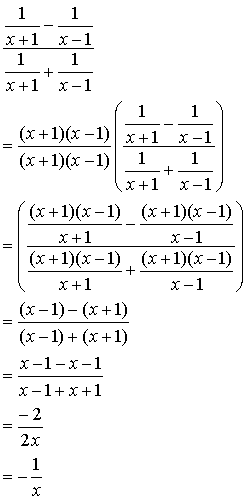 |  |  |
 | ||
 |  |  |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
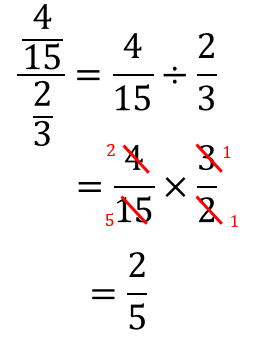 |  |  |
 |  |  |
 | ||
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 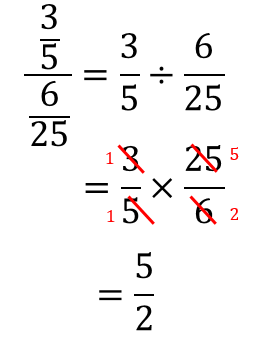 | |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 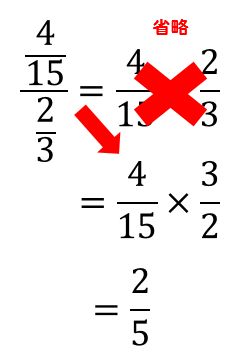 | |
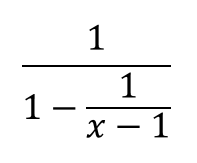 |  |  |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | 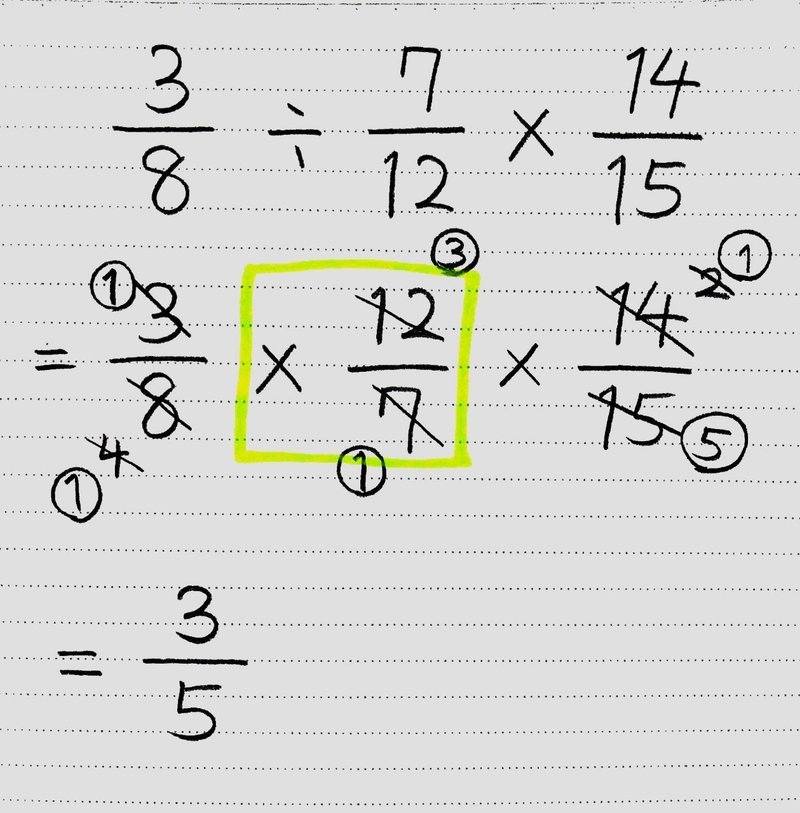 | |
「分数の解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
一次分数関数 y=\dfrac {cxd} {axb} y = ax bcxd のグラフを書く際に,上記の変形が役に立ちます: 一次分数関数のグラフと漸近線 分数式を微分したり積分したりする際も,上記の個別の頁からの質問に対する回答分数不等式の解き方について/1764 例えば,分子2 分母x-1 < x の場合はどうなりますか =>作者: 連絡ありがとう.以下,質問が であるものとして回答しま
Incoming Term: 分数の解き方, 分数の解き方 足し算, 分数の解き方 掛け算, 分数の解き方 割り算, 分数の解き方 引き算, 分数の解き方 約分, 方程式 分数の解き方, 連立方程式 分数の解き方, 一次方程式 分数の解き方, ルート 分数の解き方,
コメント
コメントを投稿